Image Resampling Tutorial

Table of Contents

• Introduction
• Example 1: SLC resampling
• Example 2: SLC resampling with carrier phase and flattening

Introduction

One of the key operations for SLC co-registration is resampling SLC images from one geometry to another. Resampling is the process of moving pixels from one place in an image to another in a new image while accounting for fractional pixel indices via interpolation. Currently, we represent the transformation with a pixel-by-pixel map of "range" offsets (i.e., offsets in the horizontal direction) and "azimuth" offsets (i.e., offsets in the vertical direction):

\[ I^\prime\left(x, y\right) = I\left(x, y, \Delta x, \Delta y\right) \]

where \(I^\prime()\) represents the resampled image, \(I()\) represents the original image, \(x\) and \(y\) are the image coordinates in the output geometry, and \(\Delta x\) and \(\Delta y\) are the offsets between the input and output geometries. For SLC co-registration, in addition to resampling of the complex pixel data, the user may also need to account for non-zero carrier phases in the azimuth direction (e.g., for native Doppler images) and flattening of the complex phase to account for differences in center frequency between the image and a master image. The isce3::image::ResampSlc class contains all relevant operations for SLC co-registration.

Example 1: SLC resampling

For the basic task of image resampling without carrier phase or flattening considerations, let's look at the following example. Here, we have a crop of an Envisat SLC, azimuth offsets that represent a contraction of the image in the vertical dimension, and range offsets that represent a shearing in the horizontal dimension.

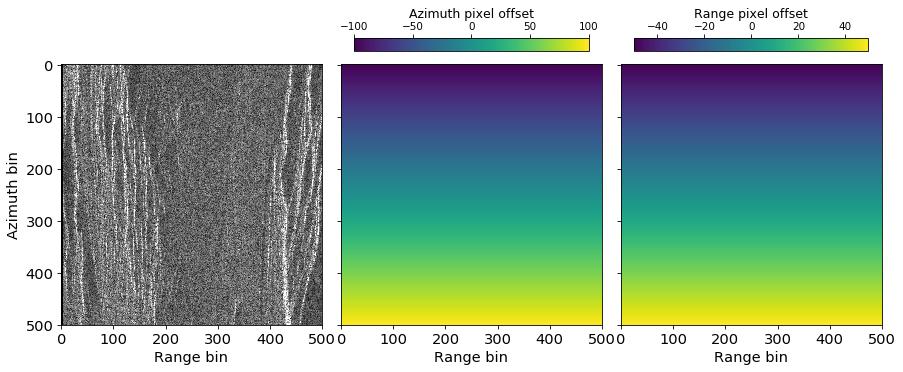
The following is example code to perform the resampling.

#include <isce3/image/ResampSlc.h>

int main() {

    // Instantiate a ResampSlc object
    isce3::image::ResampSlc resamp;

    // Open rasters for input files
    isce3::io::Raster inputSlc("input.slc");
    isce3::io::Raster rgOff("range.off");
    isce3::io::Raster azOff("azimuth.off");

    // Create raster for output resampled SLC
    isce3::io::Raster outputSlc("output.slc", rgOff.width(), rgOff.length(), 1,
                               GDT_CFloat32, "ISCE");

    // Re-run resamp
    resamp.resamp(inputSlc, outputSlc, rgOff, azOff, 1);

    return 0;
}

First, we created isce3::io::Raster objects for all input rasters: the input SLC image, the pixel-by-pixel range offsets, and the pixel-by-pixel azimuth offsets. We then created an output SLC image with the output geometry determined by the either the range or azimuth offset raster. These objects are then passed to a default isce3::image::ResampSlc instance to perform the resampling. After resampling, we obtain the following image:

Example 2: SLC resampling with carrier phase and flattening

If the user wishes to account for SLCs with native Doppler frequencies in the azimuth direction and flattening with respect to a master SLC, the following code can be used.

// isce3::core
#include <isce3/core/Poly2d.h>
// isce3::product
#include <isce3/product/ImageMode.h>
// isce3::image
#include <isce3/image/ResampSlc.h>

int main() {

    // Create polynomial for native Doppler
    // Note: 0th order in azimuth, 2nd order in range
    isce3::core::Poly2d doppler(2, 0, 0.0, 0.0, 1.0, 1.0);
    doppler.coeffs = {301.35306906319204, -0.04633312447837377, 2.044436266418998e-06};

    // Create an ImageMode for the input image using Envisat parameters
    isce3::product::ImageMode mode;
    // Set relevant parameters
    mode.wavelength(0.056);
    mode.startingRange(826988.69);
    mode.rangePixelSpacing(7.80);
    mode.prf(1652.416);

    // Create an ImageMode for the reference master image
    isce3::product::ImageMode modeRef;
    // Set relevant parameters for reference
    modeRef.wavelength(0.057);
    modeRef.startingRange(826991.0);
    modeRef.rangePixelSpacing(7.80);
    modeRef.prf(1652.416);

    // Instantiate a ResampSlc object
    isce3::image::ResampSlc resamp(doppler, mode);
    // Feed it a reference mode
    resamp.refImageMode(modeRef);

    // Open rasters for input files
    isce3::io::Raster inputSlc("input.slc");
    isce3::io::Raster rgOff("range.off");
    isce3::io::Raster azOff("azimuth.off");

    // Create raster for output resampled SLC
    isce3::io::Raster outputSlc("output.slc", rgOff.width(), rgOff.length(), 1,
                               GDT_CFloat32, "ISCE");

    // Re-run resamp
    resamp.resamp(inputSlc, outputSlc, rgOff, azOff, 1);

    return 0;
}